The electronic conduction channel constitutes the elementary building block of quantum conductors. A fascinating many-body quantum physics arises from the interactions between electrons transferred across individual quantum channels, and the circuit macroscopic quantum degrees of freedom, such as the charge in a metallic node.
The quantum electrodynamics at work results in electrical and thermal properties markedly different from those of the constitutive quantum channels. Apprehending these quantum laws has direct implications for the quantum engineering in the future nanoelectronics.
Remarkably, such quantum circuits composed of a few distinct conduction channels also provide powerful test-beds for the strongly-correlated electron physics, including the quantum criticality that develops in the vicinity of quantum phase transitions, the correlated 1D (Luttinger liquid) physics and the Kondo-type physics.

Figure 1: The central metallic island (bright) forms a circuit node of a quantum circuit. It is electrically connected through several quantum conductors tuned by field effect using voltage biased gates (blue, green and yellow).
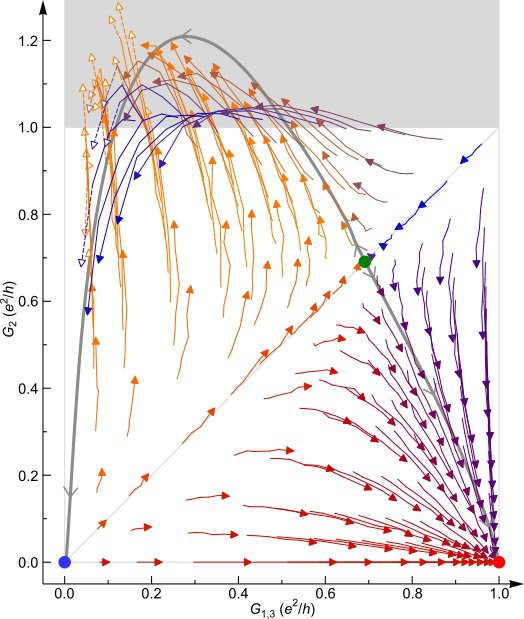
Figure 2: Development of a quantum phase transition observed through the temperature evolution of the conductance across three quantum point contacts connected to a small metallic island.
Observing the universal screening of a Kondo impurity
C. Piquard, P. Glidic, C. Han, A. Aassime, A. Cavanna, I. Gennser, Y. Meir, E. Sela, A. Anthore, F. Pierre.
Nature communications 14, 7263 (2023); arXiv:2303.12039
Probing single-electron scattering through a non-Fermi liquid charge-Kondo device
E. Sela, D. Goldhaber-Gordon, A. Anthore, F. Pierre, Y. Oreg
Physical Review B 107, L161108 (2023); arXiv:2302.02295
Cross-Correlation Investigation of Anyon Statistics in the ν=1/3 and 2/5 Fractional Quantum Hall States
P. Glidic, O. Maillet, A. Aassime, C. Piquard, A. Cavanna, U. Gennser, Y. Jin, A. Anthore, F. Pierre
Physical Review X 13, 011030 (2023); arXiv:2210.01054
Quasiparticle Andreev scattering in the ν= 1/3 fractional quantum Hall regime
P. Glidic, O. Maillet, C. Piquard, A. Aassime, A. Cavanna, Y. Jin, U. Gennser, A. Anthore, F. Pierre
Nature Communications 14, 514 (2023); arXiv:2206.08068
Fractional Entropy of Multichannel Kondo Systems from Conductance-Charge Relations
C. Han, Z. Iftikhar, Y. Kleeorin, A. Anthore, F. Pierre, Y. Meir, A.K. Mitchell, E. Sela
Physical Review Letters 128, 146803 (2022)
Universality at work - the local sine-Gordon model, lattice fermions, and quantum circuits
A. Anthore, D.M. Kennes, E. Boulat, S. Andergassen, F. Pierre, V. Meden
European Physical Journal Special Topics 229, 663 (2020)
Transmitting the quantum state of electrons across a metallic island with Coulomb interaction
H. Duprez, E. Sivre, A. Anthore, A. Aassime, A. Cavanna, U. Gennser, F. Pierre
Science 366, 1243 (2019)
Macroscopic electron quantum coherence in a solid-state circuit
H. Duprez, E. Sivre, A. Anthore, A. Aassime, A. Cavanna, A. Ouerghi, U. Gennser, F. Pierre
Phys. Rev. X 9, 021030 (2019)
Circuit Quantum Simulation of a Tomonaga-Luttinger Liquid with an Impurity
A. Anthore, Z. Iftikhar, E. Boulat, F.D. Parmentier, A. Cavanna, A. Ouerghi, U. Gennser, F. Pierre
Phys. Rev. X 8, 031075 (2018)
Physics Viewpoint: Physics 11, 94 (2018)
Tunable Quantum Criticality and Super-ballistic Transport in a 'Charge' Kondo Circuit
Z. Iftikhar, A. Anthore, A.K. Mitchell, F.D. Parmentier, U. Gennser, A. Ouerghi, A. Cavanna, C. Mora, P. Simon, F. Pierre
Science 360, 1315 (2018)
Controlling charge quantization with quantum fluctuations
S. Jezouin, Z. Iftikhar, A. Anthore, F.D. Parmentier, U. Gennser, A. Cavanna, A. Ouerghi, I.P. Levkivskyi, E. Idrisov, E.V. Sukhorukov, L.I. Glazman, F. Pierre
Nature 536, 58 (2016)
Nature News & Views: Nature 536, 38 (2016)
Two-channel Kondo effect and renormalization flow with macroscopic quantum charge states
Z. Iftikhar, S. Jezouin, A. Anthore, U. Gennser, F.D. Parmentier, A. Cavanna, F. Pierre
Nature 526, 233 (2015)
Nature News & Views: Nature 526, 203 (2015)
Tomonaga-Luttinger physics in electronic quantum circuits
S. Jezouin, M. Albert, F.D. Parmentier, A. Anthore, U. Gennser, A. Cavanna, I. Safi, F. Pierre
Nature Commun. 4, 1802 (2013)
Strong back-action of a linear circuit on a single electronic quantum channel
F.D. Parmentier, A. Anthore, S. Jezouin, H. le Sueur, U. Gennser, A. Cavanna, D. Mailly and F. Pierre
Nature Physics 7, 935 (2011)
Experimental Test of the Dynamical Coulomb Blockade Theory for Short Coherent Conductors
C. Altimiras, U. Gennser, A. Cavanna, D. Mailly, F. Pierre
Phys. Rev. Lett. 99, 256805 (2007)